O Defeito de Massa na Espectrometria de Massas

Por Oscar Vega Bustillos*

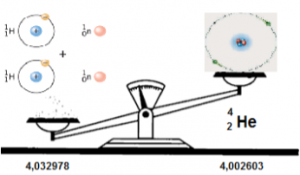
Em aritmética, a soma é definida como o resultado que se obtém quando é adicionado dois ou mais números.  Porém, na espectrometria de massas a soma não funciona assim. A soma de todas as massas das partículas fundamentais (próton, nêutron e elétron) separadamente, não corresponde á massa do átomo formado (Figura 1).  Por exemplo, a massa do átomo do Hélio, analisada por um espectrômetro de massas de alta resolução é igual a 4,002603 u. (unidades de massa atômica).  Adicionando as massas de dois prótons, dois nêutrons e dois elétrons, podemos formar um átomo de Hélio (42He).  Adicionando duas vezes o número 1,007276 (massa do próton), mais duas vezes o número 1,008665 (massa do nêutron), mais duas vezes o número 0,000548 (massa do elétron), o resultado da soma será 4,032978 u.  Diferente da massa analisada pelo espectrômetro de massas, sendo a diferença de 0,030375 u.  Esta diferença é chamada na física de defeito de massas nuclear.  A natureza utiliza esta diferença de massa para unir os núcleons na formação do átomo de Hélio.  Este defeito de massa é denominado na física nuclear como energia de ligação, isto é, a natureza utiliza um pedaço de massa dos núcleons para convertê-la em energia de união ou ligação do núcleo coeso e sem repulsão ou separação.  Este fenômeno é explorado poeticamente por muitos admiradores da natureza.  Quem descobriu esta esplendida dedução atómica foi nada menos que Albert Einstein em 1905 em seu esplendido trabalho sobre a relatividade [1].

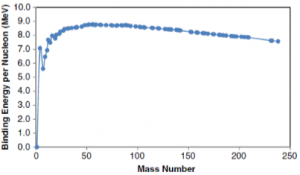
A energia de ligação é o equivalente de energia do defeito de massa de acordo com a teoria de equivalência de energia de massa de Einstein.  A energia de ligação nuclear é a fonte de energia do sol e de usinas nucleares.  A equação da Física Moderna E=mc2 encontrada na “Teoria da Relatividade”, foi desenvolvida pelo físico alemão Albert Einstein.  Esta equação determina a relação da transformação da massa de um objeto em energia e vice-versa, onde “E” representa a energia, “m” a massa e “c” a velocidade da luz, considerada a única constante do Universo.  Sabendo que a velocidade da luz é de aproximadamente 300.000 km/s, a Teoria da Relatividade pressupõe que, caso uma massa conseguisse superar a velocidade da luz, ela ultrapassaria a barreira da quarta dimensão tempo-espaço.  A Figura 2 apresenta a energia de ligação dos núcleons em função da massa dos isótopos mais abundantes.  Iniciando com o Hidrogênio e passando para átomos mais pesados, observamos que a energia de ligação por núcleon aumenta e atinge um máximo em torno de 56, o número de massa do Ferro.  Além do Ferro, a energia de ligação por núcleon diminui gradualmente. Portanto, os núcleons de massa média são os mais estáveis. Assim, o Ferro tem a maior energia de ligação sendo o núcleo mais estável.

O conceito de defeito de massa nuclear e a energia de ligação surgem no início do século 20, logo após que os pesos atômicos foram determinados com precisão por métodos químicos. Os desvios das massas atômicas dos números inteiros foram investigados por espectrometria de massas.

Defeito de massa na química, definida como a diferença entre a massa monoisotópica e a massa nominal, medido por meio de um espectro de massa de uma amostra complexa, tornou-se um critério útil para classificar e identificar os compostos de interesse entre muitos picos de íons não relacionados. Isto foi utilizado pela primeira vez para visualizar e identificar diferentes classes de compostos em amostras de petróleo e, posteriormente, aplicações encontradas em estudos de metabolismo e farmacocinética de drogas com a identificação de compostos endógenos em amostras biológicas complexas [2].

Os defeitos de massa nuclear e química são ambos causados ​​pela força nuclear forte. No entanto, apesar de sua origem comum e relacionamento próximo, são conceitos diferentes.  O defeito de massa na física nuclear é um parâmetro absoluto, enquanto o defeito de massa na química é um valor relativo.  Defeito de massa nuclear e energia de ligação são propriedades intrínsecas com valores fixos para um certo átomo. Por outro lado, o defeito da massa química não é um defeito de valor e depende da escala de massa. Defeito de massa nuclear reflete uma propriedade física, enquanto o defeito da massa química é uma convenção em que o carbono tem defeito de massa igual a zero. Considerando as diferenças entre os defeitos de massa nuclear e defeitos de massa química, propõe-se para se referir a este último como excesso de massa. Isso eliminará a confusão em torno do uso do termo defeito de massa, especialmente entre diferentes disciplinas e irá harmonizar as terminologias utilizadas em física nuclear e espectrometria de massa.

Referindo-se ao defeito de massa nuclear e química simplesmente como defeito em massa pode causar alguma confusão semântica, especialmente quando discutido entre um público mais amplo de diferentes disciplinas. Por exemplo, o defeito da massa nuclear para o carbono-12 (12C) é 0,1 u. que quando convertida em energia é igual à energia de ligação do núcleo (prótons e nêutrons no núcleo) de 7,7 Mega-elétrons Volts (MeV) para um átomo de carbono. Por outro lado, 12C com a massa atômica de 12,0000 u. (selecionado como um valor inteiro, por convenção, para definir a escala de unidade de massa atômica) tem um defeito de massa química de zero quando tratada pela análise espectral de massa e isso pode ser incorreto se for interpretado como o equivalente à energia de ligação zero para o carbono.

Enquanto defeito de massa nuclear reflete uma propriedade física, o defeito de massa química não é e se baseai em uma convenção de que o carbono tem um defeito de massa de zero. Propõe-se que se refira ao defeito de massa química como excesso de massa, a fim de eliminar a confusão em torno do uso do termo defeito de massa.

Por que as massas atômicas não são números inteiros? A missão de responder a esta pergunta e avaliar a divergência nas massas atômicas de números inteiros levaram ao conceito nuclear de defeito de massa e energia de ligação.  Mais tarde, na química, o defeito de massa desempenhou um papel importante na análise espectral de massas.

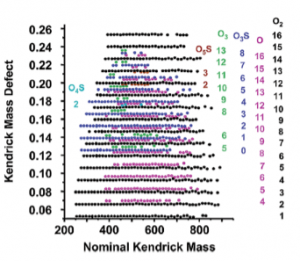
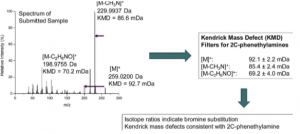
A massa de Kendrick é usada para auxiliar na identificação de moléculas de estrutura química semelhante a partir de picos em espectros de massa.  O método de determinação da massa foi sugerido em 1963 pelo químico Edward Kendrick.  A massa de Kendrick é obtida multiplicando a massa medida por um fator numérico (Figura 3).  Para sistemas de hidrocarbonetos, é utilizada uma conversão simples entre a massa exata de uma unidade de metileno (CH2) para a massa nominal de CH2. Todos os valores m/z são multiplicados pela razão 14,0000/14,01565, simplificando ainda mais a exibição e fazendo padrões de pico retilíneos aparentes para compostos do mesmo tipo, mas com diferentes comprimentos de cadeia no mesmo eixo vertical [3].  A Figura 4 apresenta análise da fenetilamina, conhecida como “hormônio da paixão”, via GC-TOFMS. Os dados de massas foram usados para desenvolver filtros do defeito de massa Kendrick com base no íon molecular e perdas neutras observadas em 2C-fenetilaminas.

Fonte: http://vegascience.blogspot.com

Figura 1: A soma de todas as massas das partículas fundamentais, (dois prótons, dois nêutrons e dois elétrons) separadamente, é de 4,032978 u. Mas, não corresponde á massa do átomo de Hélio formado (42He) de 4,002603 u. Esta diferença é denominada “defeito de massa” e corresponde á energia de ligação no núcleo atômico definida pela equação E = m c2.

Fonte: J. Am. Soc. Mass Spectrom. (2017) 28:1836-1843

Figura 2: Energia de ligação dos núcleons em função da massa dos isótopos mais abundantes.  O máximo é da massa 56 correspondente ao átomo de Ferro.

Fonte: J. Am. Soc. Mass Spectrom. (2017) 28:1836-1843

Figura 3:  Defeito de massa Kendrick versus massa nominal Kendrick para cerca de 1000 picos de íons de massa ímpar de um ESI/FT-ICR espectro de massas de uma amostra de petróleo bruto.

Fonte:  https://www.sciencedirect.com/science/article/abs/pii/S2468170917301169

Figura 4: Análise da fenetilamina via GC-TOFMS. Os dados de massas foram usados para desenvolver filtros do defeito de massa Kendrick com base no íon molecular e perdas neutras observadas em 2C-fenetilaminas.

Referências bibliográficas

W. Isaacson. “Einstein”. Ed. Companhia Das Letras. 2008.
S. Pourshahian. “Mass defect from nuclear physic to mass spectral analysis”. J. Am. Soc. Mass Spectrom. 28: 1836. 2017.
L. Sleno. “The use of mass defect in modern mass spectrometry”. J. Mass Spectrom. 47, 226. 2012.

*Oscar Vega Bustillos

Pesquisador do Centro de Química e Meio Ambiente CQMA do Instituto de Pesquisas Energéticas e Nucleares IPEN/CNEN-SP

55 11 28105656

ovega@ipen.br

www.vegascience.blogspot.com.br